
GERAK LURUS BERUBAH BERATURAN (GLBB)
Pernahkah anda melemparkan bola vertikal ke atas? Bagaimana kecepatan bola tersebut makin ke atas? Demikian pula jika sebuah bola diluncurkan di atas bidang miring, apa yang terjadi pada bola tersebut? Pernah pulakah anda menjatuhkan sebuah batu pada ketinggian tertentu? Apa yang terjadi pada kecepatan atau kelajuan bola tersebut?
Pada pembahasan kali ini, anda diharapkan mampu mengemukakan pengertian gerak lurus berubah beraturan, menganalisis besaran fisika pada gerak lurus berubah beraturan, dan mampu memformulasikan persamaan-persamaan yang ada pada gerak lurus berubah beraturan.
Peristiwa-peristiwa yang telah disebutkan diatas mengalami perubahan kecepatan secara teratur pada lintasan lurus. Perubahan disini dapat berupa penambahan kecepatan atau pengurangan kecepatan. Penambahan kecepatan disebut percepatan, sedangkan pengurangan kecepatan disebut perlambatan. Mobil yang mulai berjalan merupakan contoh gerak dipercepat, sedangkan mobil yang rem merupakan contoh gerak diperlambat. Karena lintasannya berupa garis lurus dan pertambahan atau pengurangan kecepatan dalam selang waktu yang sama adalah tetap, dapat dikatakan besar percepatannya konstan (a = tetap/konstan). Dari fenomena dan penjelasan diatas, anda telah dapat mendefinisikan pengertian dan ciri ciri dari Gerak Lurus Berubah Beraturan (GLBB). Dapatkah anda menyebutkan contoh gerak dipercepat atau diperlambat yang lainnya?
1) Percepatan Rata- Rata
Apa yang terjadi jika sebuah bola diletakkan pada papan miring? Tentu saja bola tersebut akan bergerak turun dengan kecepatan semakin besar. Benda dalam geraknya mengalami perubahan kecepatan dikatakan mengalami percepatan. Perubahan kecepatan yang dialami bola berubah secara teratur atau dengan kata lain, percepatan bola tetap (konstan). Misalnya percepatan bola 2 m/s2 dari keadaan diam diatas bidang miring. Apakah makna dari 2 m/s2?
Sesuai dengan makna percepatan yaitu pertambahan kecepatan secara teratur. Bola yang memiliki percepatan 2 m/s2 dari keadaan diam (kecepatan awal nol) artinya bahwa tiap 1 sekonnya, kecepatannya bertambah 2 m/s dan begitu seterusnya secara teratur. Perhatikan tabel dibawah :
Jika dibuat dalam bentuk grafik, maka akan diperoleh hubungan antara kecepatan (v)
dan waktu tempuh (t).
dan waktu tempuh (t).
Dengan cara yang sama dengan untuk memperoleh kecepatan (v) pada GLB maka dapat diperoleh formulasi percepatan (𝑎) = 𝑣/𝑡, dimana v adalah kecepatan dalam satuan meter per sekon (m/s) dan t adalah waktu dalam satuan sekon (s). Sekarang anda telah dapat mengetahui makna dari percepatan suatu benda. Hal sama juga berlaku untuk perlambatan. Suatu benda bergerak dengan kecepatan yang berubah-ubah dengan perubahan kecepatan yang tidak teratur maka benda tersebut mempunyai percepatan yang berubah-ubah pula. Dengan demikian anda dapat menentukan percepatan rata-ratanya.
2) Kecepatan Sesaat
Bagaimana cara menghitung kecepatan seorang pengendara motor pada saat tertentu, misalnya pada sekon ke-5? Dalam hal ini, kecepatan sesaat pada saat itu (sekon ke-5) disebut kecepatan sesaat. Kecepatan sesaat dapat dihitung berdasarkan rumus kecepatan rata-rata dengan harga ∆t (selang waktu) sangat kecil mendekati 0 (∆t → 0). Demikian juga dengan kelajuan. Kecepatan sesat merupakan turunan atau diferensial (dt/dx).
Bagaimana cara menghitung kecepatan seorang pengendara motor pada saat tertentu, misalnya pada sekon ke-5? Dalam hal ini, kecepatan sesaat pada saat itu (sekon ke-5) disebut kecepatan sesaat. Kecepatan sesaat dapat dihitung berdasarkan rumus kecepatan rata-rata dengan harga ∆t (selang waktu) sangat kecil mendekati 0 (∆t → 0). Demikian juga dengan kelajuan. Kecepatan sesat merupakan turunan atau diferensial (dt/dx).
Contoh :
Sebuah benda yang bergerak merupakan sebuah fungsi kedudukan terhadap waktu yang dinyatakan dengan persamaan
dengan x dalam meter dan t dalam sekon. Tentukan kecepatan pada saat t = 2 sekon.Sebuah benda yang bergerak merupakan sebuah fungsi kedudukan terhadap waktu yang dinyatakan dengan persamaan
Jawab.
Dengan menggunakan perhitungan diferensial, dapat diselesaikan dengan cara dengan mudah.
Telah diperoleh persamaan kecepatan saat t sekon. Sehingga kecepatan saat 2 sekon (t=2 sekon)
3) Percepatan Sesaat
Percepatan sesaat identik dengan kecepatan sesaat yang merupakan perubahan kedudukan dalam selang waktu yang sangat kecil. Perubahan kecepatan dalam selang waktu yang sangat kecil dinamakan percepatan sesaat. Percepatan sesaat dapat dengan mudah diperoleh sebagai turunan dari kecepatan 𝑎 = 𝑑𝑣/𝑑𝑡
Contoh :
Sepeda motor bergerak mengikuti persamaan kecepatan sebagai fungsi waktu
dengan v dalam m/s dan t dalam sekon. Tentukan percepatan sesaat pada t = 3 s.Percepatan sesaat identik dengan kecepatan sesaat yang merupakan perubahan kedudukan dalam selang waktu yang sangat kecil. Perubahan kecepatan dalam selang waktu yang sangat kecil dinamakan percepatan sesaat. Percepatan sesaat dapat dengan mudah diperoleh sebagai turunan dari kecepatan 𝑎 = 𝑑𝑣/𝑑𝑡
Contoh :
Sepeda motor bergerak mengikuti persamaan kecepatan sebagai fungsi waktu
Jawab.
Dengan menggunakan perhitungan diferensial, dapat diselesaikan dan diperoleh hasil yaitu:
Dengan menggunakan perhitungan diferensial, dapat diselesaikan dan diperoleh hasil yaitu:
Telah diperoleh persamaan kecepatan saat t sekon. Sehingga kecepatan saat 2 sekon
4) Gerak lurus berubah beraturan (GLBB)
Telah dijelaskan sebelumnya bahwa suatu benda dikatakan melakukan Gerak Lurus Berubah Beraturan (GLBB) jika kecepatan geraknya berubah secara teratur (a=0). Perubahannya dapat berupa penambahan kecepatan (percepatan) atau pengurangan kecepatan (perlambatan).
Contoh 1 :
Misalkan bola dengan kecepatan awal 3 m/s dan mengalami percepatan sebesar mengalami percepatan sebesar 2 m/s2. Berapa besar kecepatan bola setelah 4 sekon?
Jawab.
Sketsa dari kasus diatas dapat digambarkan sebagai berikut :
Telah dijelaskan sebelumnya bahwa suatu benda dikatakan melakukan Gerak Lurus Berubah Beraturan (GLBB) jika kecepatan geraknya berubah secara teratur (a=0). Perubahannya dapat berupa penambahan kecepatan (percepatan) atau pengurangan kecepatan (perlambatan).
Contoh 1 :
Misalkan bola dengan kecepatan awal 3 m/s dan mengalami percepatan sebesar mengalami percepatan sebesar 2 m/s2. Berapa besar kecepatan bola setelah 4 sekon?
Jawab.
Sketsa dari kasus diatas dapat digambarkan sebagai berikut :
Percepatan 2 m/s2 artinya tiap detik kepatannya akan bertambah 2 m/s, sehingga untuk :
0 sekon, kecepatannya = 3 m/s = V0 (kecepatan mula-mula)
1 sekon, kecepatannya = 5 m/s = 3 m/s + 2 m/s = V0 + a
2 sekon, kecepatannya = 7 m/s = 3 m/s + 2(2) m/s = V0 + 2a
3 sekon, kecepatannya = 9 m/s = 3 m/s + 3(2) m/s = V0 + 3a,
4 sekon, kecepatannya = 11 m/s = 3 m/s + 4(2) m/s = V0 + 4a dan seterusnya
Jadi kecepatan setelah 4 sekon adalah 11 m/s.
Dari uraian diatas, diperoleh pola pertambahan kecepatan setiap waktu. Sehingga untuk t sekon kecepatan akhirnya (Vt) :
Keterangan : 0 sekon, kecepatannya = 3 m/s = V0 (kecepatan mula-mula)
1 sekon, kecepatannya = 5 m/s = 3 m/s + 2 m/s = V0 + a
2 sekon, kecepatannya = 7 m/s = 3 m/s + 2(2) m/s = V0 + 2a
3 sekon, kecepatannya = 9 m/s = 3 m/s + 3(2) m/s = V0 + 3a,
4 sekon, kecepatannya = 11 m/s = 3 m/s + 4(2) m/s = V0 + 4a dan seterusnya
Jadi kecepatan setelah 4 sekon adalah 11 m/s.
Dari uraian diatas, diperoleh pola pertambahan kecepatan setiap waktu. Sehingga untuk t sekon kecepatan akhirnya (Vt) :
Vt = kecepatan saat t sekon (m/s)
Vo = kecepatan mula-mula (m/s)
a = percepatan (m/s2)
t = waktu (s)
a = percepatan (m/s2)
t = waktu (s)
Contoh 2 :
Sebuah benda bergerak lurus dengan besar kecepatan awal 10 m/s. benda tersebut diberi percepatan sebesar 2 m/s2. Tentukan besar kecepatan dan jarak yang ditempuh saat benda tersebut telah bergerak 5 sekon.
Jawab.
Sketsa dari kasus diatas dapat digambarkan sebagai berikut
Sebuah benda bergerak lurus dengan besar kecepatan awal 10 m/s. benda tersebut diberi percepatan sebesar 2 m/s2. Tentukan besar kecepatan dan jarak yang ditempuh saat benda tersebut telah bergerak 5 sekon.
Jawab.
Sketsa dari kasus diatas dapat digambarkan sebagai berikut
Percepatan 2 m/s2 artinya tiap detik kepatannya akan bertambah 2 m/s, sehingga
untuk :
0 sekon, kecepatannya = 10 m/s = V0 (kecepatan mula-mula)
1 sekon, kecepatannya = 12 m/s = 10 m/s + 2 m/s = V0 + a
2 sekon, kecepatannya = 14 m/s = 10 m/s + 2(2) m/s = V0 + 2a
3 sekon, kecepatannya = 16 m/s = 10 m/s + 3(2) m/s = V0 + 3a,
4 sekon, kecepatannya = 18 m/s = 10 m/s + 4(2) m/s = V0 + 4a
5 sekon, kecepatannya = 20 m/s = 10 m/s + 5(2) = V0 + 5a dan seterusnya
Jadi kecepatan setelah 5 sekon adalah 20 m/s.
untuk :
0 sekon, kecepatannya = 10 m/s = V0 (kecepatan mula-mula)
1 sekon, kecepatannya = 12 m/s = 10 m/s + 2 m/s = V0 + a
2 sekon, kecepatannya = 14 m/s = 10 m/s + 2(2) m/s = V0 + 2a
3 sekon, kecepatannya = 16 m/s = 10 m/s + 3(2) m/s = V0 + 3a,
4 sekon, kecepatannya = 18 m/s = 10 m/s + 4(2) m/s = V0 + 4a
5 sekon, kecepatannya = 20 m/s = 10 m/s + 5(2) = V0 + 5a dan seterusnya
Jadi kecepatan setelah 5 sekon adalah 20 m/s.
Seperti yang telah kita ketahui bersama pada GLB bahwa jarak dapat ditentukan dengan persamaan s = v.t. Untuk kasus diatas merupakan GLBB dipercepat dimana kecepatan benda bertambah setiap saat secara teratur. Sehingga kecepatan yang digunakan adalah kecepatan rata-rata (𝑣).
Anda dapat memparoleh persamaan baru untuk menghitung jarak (s) tiap waktu (t) pada GLBB dengan cara :
Dengan mengsubtitusi pers. 1 ke pers. 2 maka akan diperoleh :
Contoh 3 :
Sebuah mobil yang melaju dengan kecepatan 54 km/jam tiba-tiba direm dengan perlambatan 3 m/s. Berapa besar waktu dan jarak setelah pengereman hingga mobil berhenti?
Jawab.
Sebuah mobil yang melaju dengan kecepatan 54 km/jam tiba-tiba direm dengan perlambatan 3 m/s. Berapa besar waktu dan jarak setelah pengereman hingga mobil berhenti?
Jawab.
Sketsa dari kasus diatas dapat digambarkan sebagai berikut
0 sekon, kecepatannya = 15 m/s = V0 (kecepatan mula-mula)
1 sekon, kecepatannya = 12 m/s = 15 m/s - 3 m/s = Vo - a
2 sekon, kecepatannya = 9 m/s = 15m/s - 2(3) m/s = Vo - 2a
3 sekon, kecepatannya = 6 m/s = 15 m/s - 3(3) m/s = Vo - 3a,
4 sekon, kecepatannya = 3 m/s = 15 m/s - 4(3) m/s = Vo - 4a
5 sekon, kecepatannya = 0 m/s = 15 m/s – 5(3) = Vo - 5a dan seterusnya
mobil berhenti setelah 5 sekon
Dari uraian diatas, diperoleh pola pengurangan kecepatan setiap waktu
(perlambatan). Sehingga untuk t sekon kecepatan akhirnya (vt) :
2 sekon, kecepatannya = 9 m/s = 15m/s - 2(3) m/s = Vo - 2a
3 sekon, kecepatannya = 6 m/s = 15 m/s - 3(3) m/s = Vo - 3a,
4 sekon, kecepatannya = 3 m/s = 15 m/s - 4(3) m/s = Vo - 4a
5 sekon, kecepatannya = 0 m/s = 15 m/s – 5(3) = Vo - 5a dan seterusnya
mobil berhenti setelah 5 sekon
Dari uraian diatas, diperoleh pola pengurangan kecepatan setiap waktu
(perlambatan). Sehingga untuk t sekon kecepatan akhirnya (vt) :
Kasus diatas merupakan GLBB diperlambat. Dengan cara yang sama pada contoh 2 dapat dipeoleh jarak (s) :
Dengan menggunakan pers. 1 dan pers. 3, akan diperoleh nilai yang sama. Karena benda diperlambat maka a bernilai negatif.
Jadi, mobil berhenti setelah 5 sekon
Anda dapat memperoleh formulasi persamaan baru dengan cara mengsubtitusi nilai t pada pers.1 ke pers.3. Jika anda telah melakukannya, seharusnya anda akan memperoleh persamaan :














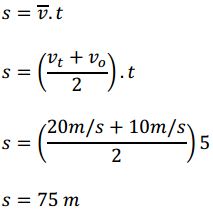









EmoticonEmoticon